3/5 As An Equivalent Fraction
odrchambers
Sep 12, 2025 · 6 min read
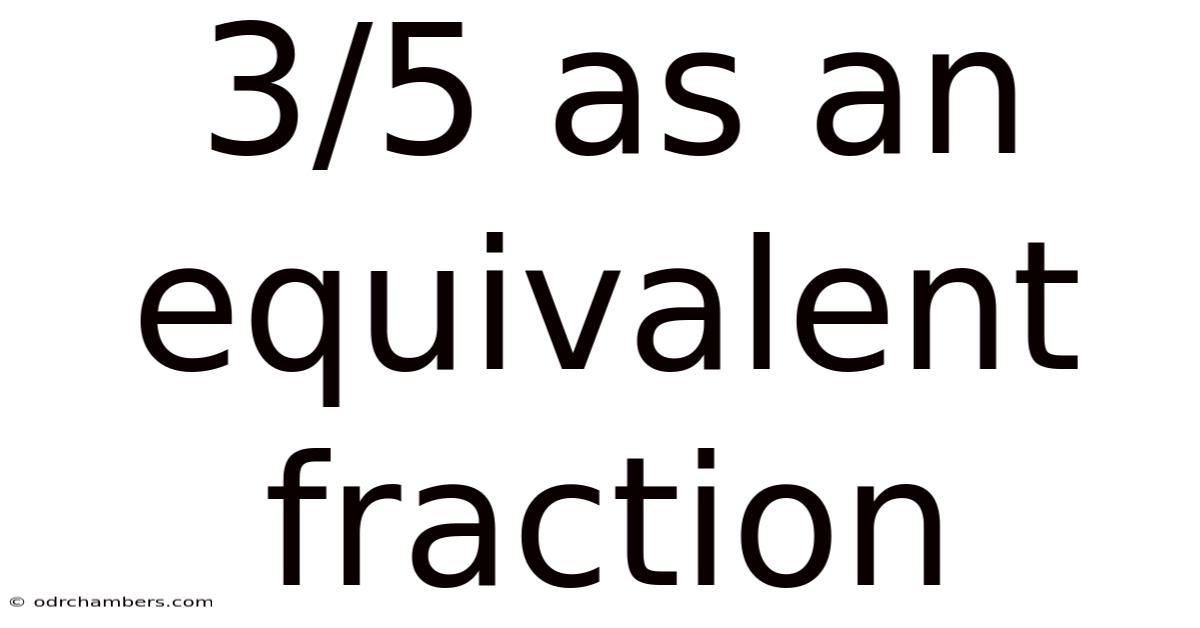
Table of Contents
Understanding 3/5: Unveiling the World of Equivalent Fractions
Fractions are fundamental building blocks in mathematics, representing parts of a whole. Understanding fractions is crucial for various aspects of life, from baking a cake to calculating financial proportions. This comprehensive guide delves into the fraction 3/5, exploring its equivalent fractions, simplifying techniques, and real-world applications. We will unravel the mystery behind equivalent fractions and show you how easily you can master this concept. This article is perfect for students, teachers, and anyone looking to solidify their understanding of fractions.
Introduction: What are Equivalent Fractions?
Before we dive into the specifics of 3/5, let's establish a strong foundation. Equivalent fractions are fractions that represent the same value, even though they look different. Imagine slicing a pizza: one-half (1/2) is the same as two-quarters (2/4), and also the same as four-eighths (4/8). These are all equivalent fractions. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant. Understanding equivalent fractions is vital for comparing, adding, and subtracting fractions effectively. We'll learn how to find equivalent fractions for 3/5 and why they are important.
Finding Equivalent Fractions for 3/5: A Step-by-Step Guide
The beauty of equivalent fractions lies in their simplicity. To find an equivalent fraction for 3/5, you simply multiply (or divide) both the numerator and the denominator by the same non-zero number. This process maintains the ratio, thus preserving the fraction's value. Let's illustrate this with some examples:
-
Multiplying by 2:
- 3/5 * 2/2 = 6/10. Therefore, 6/10 is an equivalent fraction to 3/5.
-
Multiplying by 3:
- 3/5 * 3/3 = 9/15. Thus, 9/15 is another equivalent fraction of 3/5.
-
Multiplying by 4:
- 3/5 * 4/4 = 12/20. Similarly, 12/20 is also an equivalent fraction to 3/5.
We can continue this process indefinitely, generating an infinite number of equivalent fractions for 3/5. Each fraction represents the same portion of a whole, just expressed differently.
Dividing to Find Equivalent Fractions (Simplifying Fractions)
The reverse process, dividing both the numerator and the denominator by the same non-zero number, is called simplifying or reducing a fraction to its lowest terms. While we can generate countless equivalent fractions by multiplying, simplifying helps to express the fraction in its simplest form. This makes it easier to understand and compare fractions. However, in the case of 3/5, the fraction is already in its simplest form because 3 and 5 share no common factors other than 1.
Visualizing Equivalent Fractions for 3/5
Visual representations are invaluable for grasping abstract mathematical concepts. Let's imagine a rectangle divided into five equal parts. Shading three of these parts visually represents the fraction 3/5. Now, imagine dividing each of the five parts into two equal parts. You'll now have ten smaller parts, and six of them will be shaded—this represents the equivalent fraction 6/10. Similarly, you can divide each of the five original parts into three, four, or more equal parts, always resulting in a visually equivalent fraction.
The Importance of Equivalent Fractions
The ability to identify and work with equivalent fractions is crucial for various mathematical operations:
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, you often need to find a common denominator. This involves converting the fractions into equivalent fractions with the same denominator.
-
Comparing Fractions: It’s easier to compare fractions when they have a common denominator. Equivalent fractions allow us to rewrite fractions in a form that facilitates comparison. For example, determining whether 3/5 is greater than or less than 2/3 is easier if we find equivalent fractions with a common denominator (15). 3/5 becomes 9/15, and 2/3 becomes 10/15. Now it is clear that 2/3 > 3/5.
-
Real-World Applications: Equivalent fractions are used extensively in daily life, particularly when dealing with proportions and ratios. For example, scaling recipes (increasing or decreasing ingredient amounts) involves working with equivalent fractions.
Solving Problems Using Equivalent Fractions of 3/5
Let's explore some practical examples to solidify our understanding:
Example 1: Sharing a Pizza
Imagine you have a pizza cut into 20 slices. How many slices represent 3/5 of the pizza?
Solution: We need to find an equivalent fraction of 3/5 with a denominator of 20. We multiply both the numerator and the denominator by 4: (3/5) * (4/4) = 12/20. Therefore, 12 slices represent 3/5 of the pizza.
Example 2: Calculating Proportions
A class has 25 students, and 3/5 of them are girls. How many girls are in the class?
Solution: We need to find 3/5 of 25. This is calculated as (3/5) * 25 = 15. There are 15 girls in the class.
Example 3: Recipe Scaling
A recipe calls for 3/5 of a cup of flour. If you want to double the recipe, how much flour do you need?
Solution: Doubling the recipe means multiplying the amount of flour by 2: (3/5) * 2 = 6/5, which is equal to 1 1/5 cups of flour.
Frequently Asked Questions (FAQ)
-
Q: Is 3/5 a proper or improper fraction?
- A: 3/5 is a proper fraction because the numerator (3) is smaller than the denominator (5).
-
Q: How can I tell if two fractions are equivalent?
- A: Two fractions are equivalent if their cross products are equal. For example, to check if 3/5 and 6/10 are equivalent, cross-multiply: 3 * 10 = 30 and 5 * 6 = 30. Since the cross products are equal, the fractions are equivalent.
-
Q: What is the simplest form of 3/5?
- A: 3/5 is already in its simplest form because 3 and 5 have no common factors other than 1.
-
Q: Can I find an equivalent fraction for 3/5 with a specific denominator?
- A: Yes, you can. If you want to find an equivalent fraction with a denominator of, say, 35, you would divide 35 by the original denominator (5), which gives you 7. Then, multiply both the numerator and denominator of 3/5 by 7: (3/5) * (7/7) = 21/35.
-
Q: Are there any other methods to find equivalent fractions?
- A: While multiplying and dividing by the same number is the most common method, visual representations and simplifying using the greatest common divisor (GCD) are also effective techniques.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions, particularly those related to 3/5, opens doors to a deeper comprehension of fractions as a whole. This seemingly simple concept is the bedrock of more advanced mathematical topics. By grasping the principles of multiplying and dividing both the numerator and denominator by the same number, and by understanding the importance of simplifying fractions to their lowest terms, you can confidently tackle a wide range of mathematical problems and real-world scenarios involving fractions. Remember to practice regularly to build fluency and confidence in working with equivalent fractions. With consistent effort, mastering this concept will significantly enhance your mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
Maths Extension 1 Formula Sheet
Sep 12, 2025
-
Old Man Of Hoy Location
Sep 12, 2025
-
Central West Medical Centre Braybrook
Sep 12, 2025
-
Maslows Hierarchy Of Needs Pdf
Sep 12, 2025
-
Holy Trinity Church Fortitude Valley
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3/5 As An Equivalent Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.