Cos 2x 1 Sin 2x
odrchambers
Sep 24, 2025 · 5 min read
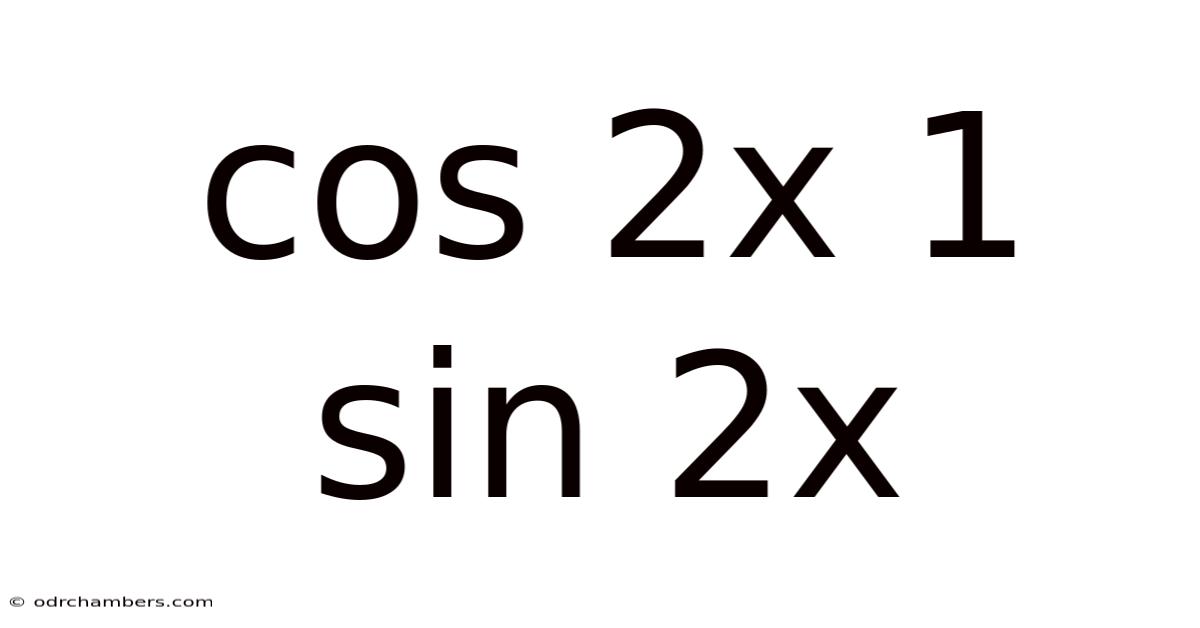
Table of Contents
Exploring the Trigonometric Expression: cos 2x + sin 2x
This article delves into the trigonometric expression cos 2x + sin 2x, exploring its properties, transformations, and applications. We will unpack its various representations, understand its behavior graphically, and examine how it can be manipulated and simplified within different mathematical contexts. Understanding this expression is crucial for anyone studying trigonometry, calculus, or related fields. We'll cover the core concepts in a clear and accessible manner, suitable for students and anyone looking to refresh their understanding of trigonometric identities. This comprehensive guide will equip you with the tools to confidently tackle problems involving this expression.
Understanding the Fundamental Trigonometric Identities
Before we dive into cos 2x + sin 2x, let's refresh our understanding of some key trigonometric identities. These identities are fundamental building blocks for manipulating and simplifying trigonometric expressions.
-
Pythagorean Identity: sin²x + cos²x = 1. This is arguably the most important identity, forming the basis for many other derivations.
-
Double Angle Identities: These identities express trigonometric functions of 2x in terms of trigonometric functions of x. The most relevant for our exploration are:
- cos 2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
- sin 2x = 2sin x cos x
-
Sum-to-Product and Product-to-Sum Identities: While not directly used in the initial simplification of cos 2x + sin 2x, these identities are crucial for more advanced manipulations and solving certain types of equations involving this expression.
Representing cos 2x + sin 2x in Different Forms
The expression cos 2x + sin 2x can be represented in several equivalent forms, each useful in different situations. The choice of representation depends on the context of the problem. Let's explore some key transformations:
1. Using Double Angle Identities:
We can directly substitute the double angle identities for cos 2x and sin 2x:
cos 2x + sin 2x = (cos²x - sin²x) + 2sin x cos x
This form, while correct, isn't inherently simpler. It's useful as a starting point for further manipulation.
2. Representing as a Single Trigonometric Function:
This is achieved through the use of a clever trigonometric manipulation. We can rewrite the expression in the form Rsin(2x + α), where R is the amplitude and α is the phase shift. This form is incredibly useful for graphing and understanding the overall behavior of the function.
To achieve this, we utilize the angle sum identity for sine: sin(A + B) = sin A cos B + cos A sin B
Let's assume cos 2x + sin 2x = R sin(2x + α) = R (sin 2x cos α + cos 2x sin α)
By comparing coefficients, we get:
R cos α = 1 and R sin α = 1
Dividing these two equations, we find: tan α = 1, which implies α = π/4 (or 45°).
Squaring and adding the two equations, we obtain: R² (cos²α + sin²α) = 1² + 1² = 2
Since cos²α + sin²α = 1, we have R² = 2, thus R = √2.
Therefore, cos 2x + sin 2x = √2 sin(2x + π/4)
This representation is significantly more insightful. It reveals that the expression is a sinusoidal wave with an amplitude of √2 and a phase shift of π/4 radians (45 degrees) to the left.
3. Alternative Form Using Cosine:
Similarly, we can express the function in the form R cos(2x - β). Following a similar process as above, we would find:
cos 2x + sin 2x = √2 cos(2x - π/4)
Graphical Representation and Analysis
The transformation into the form √2 sin(2x + π/4) or √2 cos(2x - π/4) is invaluable for visualizing the function's behavior. The graph is a sinusoidal wave with:
- Amplitude: √2 ≈ 1.414
- Period: π (half the period of sin x or cos x)
- Phase Shift: π/4 to the left (for the sine form) or π/4 to the right (for the cosine form)
This graphical representation helps understand the function's oscillations and its values at specific points. For instance, we can readily identify maximum and minimum values, zeros, and intervals of increase and decrease.
Solving Equations Involving cos 2x + sin 2x
The various representations of cos 2x + sin 2x are particularly useful in solving equations. For example, consider the equation:
cos 2x + sin 2x = 1
Using the form √2 sin(2x + π/4) = 1, we can solve for 2x + π/4:
sin(2x + π/4) = 1/√2
This gives us 2x + π/4 = π/4 + 2nπ or 2x + π/4 = 3π/4 + 2nπ, where n is an integer.
Solving for x in each case yields the general solutions for x.
Similarly, other equations involving this expression can be solved more efficiently using the single trigonometric function representations.
Applications in Calculus and Other Fields
The expression cos 2x + sin 2x appears in various applications within calculus and other fields.
-
Integration and Differentiation: The simplified forms are easier to integrate and differentiate than the original expression. The use of the single trigonometric function forms simplifies these calculus operations significantly.
-
Physics and Engineering: Oscillatory systems, wave phenomena, and other applications often involve expressions similar to cos 2x + sin 2x. The understanding of its properties is essential for modeling and analyzing such systems.
Frequently Asked Questions (FAQ)
-
Q: Can cos 2x + sin 2x ever be equal to 0?
A: Yes, the expression equals zero at specific values of x. Using the form √2 sin(2x + π/4) = 0, we find that sin(2x + π/4) = 0. This occurs when 2x + π/4 = nπ, where n is an integer. Solving for x provides the solutions where the expression is zero.
-
Q: What is the maximum value of cos 2x + sin 2x?
A: The maximum value is √2, which occurs when sin(2x + π/4) = 1.
-
Q: What is the minimum value of cos 2x + sin 2x?
A: The minimum value is -√2, which occurs when sin(2x + π/4) = -1.
-
Q: How can I prove the identity cos 2x + sin 2x = √2 sin(2x + π/4)?
A: The proof involves using the angle sum identity for sine and comparing coefficients, as detailed in the section "Representing as a Single Trigonometric Function."
Conclusion
The trigonometric expression cos 2x + sin 2x, while seemingly simple, offers a rich landscape for exploration. Its various representations, particularly the single trigonometric function forms (√2 sin(2x + π/4) and √2 cos(2x - π/4)), significantly simplify its analysis and application. Understanding its graphical behavior, along with its use in solving equations and calculus problems, makes it a vital concept in trigonometry and related fields. This comprehensive overview should equip you with a solid foundation for working with this expression effectively. Remember to practice applying these concepts to various problems to solidify your understanding. The more you work with these identities and transformations, the more intuitive they will become.
Latest Posts
Latest Posts
-
How Much Do Interlocks Cost
Sep 24, 2025
-
What Is A Cantilever Bridge
Sep 24, 2025
-
Otaa Ties And Accessories
Sep 24, 2025
-
Drills For Digging In Volleyball
Sep 24, 2025
-
What Is The Easter Triduum
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Cos 2x 1 Sin 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.