Density Mass And Volume Triangle
odrchambers
Sep 21, 2025 · 7 min read
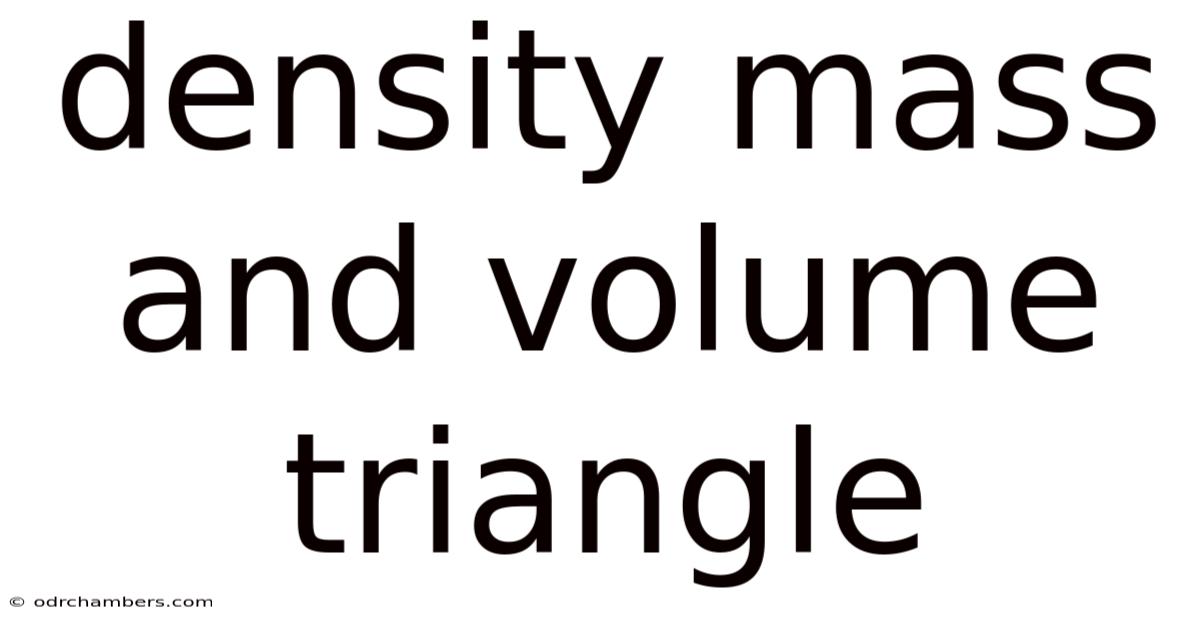
Table of Contents
Understanding the Density, Mass, and Volume Triangle: A Comprehensive Guide
The relationship between density, mass, and volume is fundamental to physics and chemistry. Understanding this relationship is crucial for solving a wide variety of problems, from determining the composition of materials to understanding fluid dynamics. This comprehensive guide will explore the concept of the "density, mass, and volume triangle," providing clear explanations, illustrative examples, and practical applications. We'll also delve into the scientific principles behind these concepts and address frequently asked questions.
Introduction: The Interconnectedness of Density, Mass, and Volume
The density, mass, and volume of an object are intrinsically linked. They are not independent properties but rather describe different aspects of the same physical entity. Think of it like a triangle where each corner represents one of these properties. Understanding the relationship between these three allows us to calculate one if we know the other two.
- Mass: Represents the amount of matter in an object. It's measured in kilograms (kg) or grams (g).
- Volume: Represents the amount of space an object occupies. It's measured in cubic meters (m³), cubic centimeters (cm³), or liters (L).
- Density: Represents the mass per unit volume of a substance. It's measured in kilograms per cubic meter (kg/m³) or grams per cubic centimeter (g/cm³).
This interconnectedness is represented mathematically by the following formula:
Density = Mass / Volume
or, ρ = m / V
where:
- ρ (rho) represents density
- m represents mass
- V represents volume
This simple equation forms the core of the density, mass, and volume triangle, allowing us to easily calculate any one of the three properties if the other two are known.
Understanding the Density, Mass, and Volume Triangle: A Visual Representation
Imagine an equilateral triangle with each corner labeled: Density, Mass, and Volume.
Density (ρ)
/ \
/ \
/ \
Mass (m)-------Volume (V)
The formula ρ = m/V is visually represented by the triangle. To find any one of the variables, cover the unknown variable with your finger. The remaining variables will show you the calculation to perform:
- To find Density (ρ): Cover ρ. You're left with m/V, indicating that Density = Mass / Volume.
- To find Mass (m): Cover m. You're left with ρ x V, indicating that Mass = Density x Volume.
- To find Volume (V): Cover V. You're left with m/ρ, indicating that Volume = Mass / Density.
This visual representation provides a quick and easy way to remember the relationships between these three crucial properties.
Practical Applications and Examples
The concept of the density, mass, and volume triangle is widely used across various scientific disciplines and everyday applications. Here are a few examples:
1. Determining the density of an irregular object:
Let's say we have a irregularly shaped rock. We can find its mass using a balance scale. To find its volume, we can use the water displacement method. We fill a graduated cylinder with a known volume of water, carefully submerge the rock, and measure the increase in water level. The difference in water levels represents the volume of the rock. Finally, we use the formula: Density = Mass / Volume to calculate the rock's density.
2. Identifying unknown substances:
Density is a characteristic property of a substance. Knowing the density of an unknown substance can help identify it by comparing it to known densities in reference tables. For instance, if you have a metal sample and determine its density to be 7.87 g/cm³, you can conclude that it is likely iron, given iron's known density.
3. Determining the buoyancy of objects:
Archimedes' principle states that an object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced. The density of the object relative to the density of the fluid determines whether the object will float or sink. An object will float if its density is less than the density of the fluid and sink if its density is greater.
4. Engineering and Construction:
In engineering and construction, understanding density is crucial for calculating the weight of materials used in structural designs, ensuring stability and safety. For example, knowing the density of concrete allows engineers to accurately estimate the weight of a bridge or building and design accordingly.
5. Environmental Science:
In environmental science, density measurements are used to monitor water quality, detect pollution, and assess the health of ecosystems. For instance, changes in water density can indicate the presence of pollutants or algal blooms.
Advanced Concepts and Considerations
While the basic formula ρ = m/V is straightforward, several important considerations can affect accuracy and understanding:
-
Temperature and Pressure: Density is temperature and pressure dependent. The density of gases, in particular, changes significantly with changes in temperature and pressure. This needs to be considered when working with gases, requiring adjustments to the basic formula or the use of more complex equations incorporating these factors. For solids and liquids, the changes are usually less significant but still important for high-precision measurements.
-
Non-uniform Density: The formula assumes uniform density throughout the object. Many objects do not have uniform densities. For instance, a wooden log may be denser in the core than at its outer edges. For such cases, more sophisticated techniques may be required to determine the average density or the density profile of the object.
-
Compressibility: The formula assumes that the volume of the object is constant. However, some materials are compressible, meaning their volume can change under pressure. This is particularly relevant for gases and to a lesser extent for liquids. In such cases, the volume used in the calculation must reflect the volume at the specific pressure under consideration.
-
Units: Always ensure consistent units throughout the calculation. Inconsistency in units can lead to significant errors. If you use kilograms for mass, you must use cubic meters for volume; otherwise, the calculation will produce an incorrect density.
Frequently Asked Questions (FAQs)
Q: What is the difference between mass and weight?
A: Mass is a measure of the amount of matter in an object, while weight is a measure of the force of gravity acting on that object. Mass remains constant regardless of location, while weight varies depending on the gravitational field strength.
Q: Can the density of a substance change?
A: While the density of a pure substance is generally constant at a given temperature and pressure, it can change with changes in temperature and pressure. The density of a mixture can also change depending on the composition of the mixture.
Q: What are some common units of density?
A: Common units of density include kg/m³, g/cm³, g/mL, and lb/ft³. The choice of unit depends on the context and the magnitude of the density being measured.
Q: How can I measure the volume of an irregularly shaped object?
A: The water displacement method is commonly used to measure the volume of irregularly shaped objects. Submerge the object in a known volume of water and measure the increase in water level. The difference represents the volume of the object.
Q: What is specific gravity?
A: Specific gravity is the ratio of the density of a substance to the density of a reference substance, typically water at 4°C. It is a dimensionless quantity and provides a convenient way to compare the relative densities of different substances.
Conclusion: The Power of the Density, Mass, and Volume Triangle
The density, mass, and volume triangle provides a simple yet powerful tool for understanding and calculating the properties of matter. By mastering the relationship between these three fundamental concepts, we can tackle a wide range of problems in various scientific fields and everyday situations. Remember the formula, visualize the triangle, and pay careful attention to units and potential factors like temperature and pressure to ensure accurate and meaningful results. Understanding this triangle is key to unlocking a deeper understanding of the physical world around us. From identifying unknown materials to designing complex structures, the principles of density, mass, and volume are essential for solving problems and advancing our knowledge across disciplines.
Latest Posts
Latest Posts
-
A Minor 7th Piano Chord
Sep 22, 2025
-
Cast Of King Cobra 1999
Sep 22, 2025
-
Zone C Flinders Medical Centre
Sep 22, 2025
-
Interesting Facts About Caroline Chisholm
Sep 22, 2025
-
Accommodation Near Ben Lomond Tasmania
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Density Mass And Volume Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.