Sin X Sin 180 X
odrchambers
Sep 13, 2025 · 6 min read
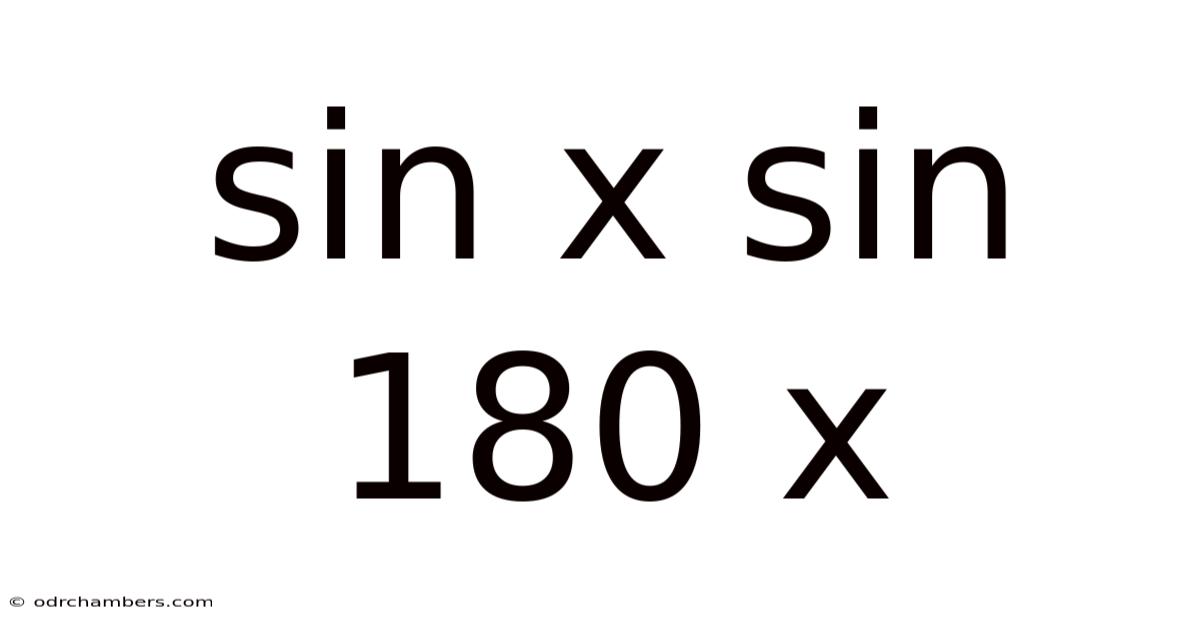
Table of Contents
Unveiling the Mystery: sin x sin (180 - x)
Understanding trigonometric identities is crucial for anyone studying mathematics, particularly in fields like calculus, physics, and engineering. This article delves deep into the intriguing relationship between sin x and sin (180° - x), exploring its mathematical proof, practical applications, and implications within a broader trigonometric context. We’ll unravel the mystery behind this identity and equip you with a solid understanding of its significance. This exploration will cover its derivation, practical uses, and frequently asked questions, making the concept accessible to students of all levels.
Introduction: The Identity and its Significance
The core of our exploration revolves around the trigonometric identity: sin x = sin (180° - x). This seemingly simple equation holds profound implications within the world of trigonometry. It highlights the symmetry and cyclical nature of sine functions, crucial for understanding wave phenomena, oscillations, and various other applications in science and engineering. Understanding this identity unlocks a deeper comprehension of angle relationships within the unit circle and simplifies complex trigonometric expressions.
Graphical Representation and Intuitive Understanding
Before diving into the mathematical proof, let's visualize the identity. Consider the unit circle, a circle with a radius of 1 centered at the origin of a coordinate plane. The sine of an angle x is defined as the y-coordinate of the point where the terminal side of the angle intersects the unit circle.
Now, consider the angle (180° - x). This angle is the reflection of angle x across the y-axis. Observe that the y-coordinate of the point where the terminal side of (180° - x) intersects the unit circle is identical to the y-coordinate of the point where the terminal side of x intersects the unit circle. This visual representation provides an intuitive grasp of why sin x = sin (180° - x).
Mathematical Proof using the Sine Difference Formula
We can rigorously prove this identity using the sine difference formula:
sin (A - B) = sin A cos B - cos A sin B
Let A = 180° and B = x. Substituting these values into the formula, we get:
sin (180° - x) = sin 180° cos x - cos 180° sin x
Since sin 180° = 0 and cos 180° = -1, the equation simplifies to:
sin (180° - x) = 0 * cos x - (-1) * sin x
sin (180° - x) = sin x
This rigorously proves the identity.
Exploring the Relationship in Different Quadrants
The identity sin x = sin (180° - x) holds true regardless of the quadrant in which angle x lies. Let’s examine this quadrant-by-quadrant:
-
Quadrant I (0° < x < 90°): Both x and (180° - x) are positive, and their sine values are positive and equal.
-
Quadrant II (90° < x < 180°): x lies in Quadrant II, where sine is positive. (180° - x) lies in Quadrant I, also where sine is positive. Again, the sine values are equal.
-
Quadrant III (180° < x < 270°): x lies in Quadrant III, where sine is negative. (180° - x) lies in Quadrant II, where sine is positive. The sine values are equal in magnitude but opposite in sign. This seemingly contradicts the identity. However, we need to remember that we are examining sin(180° - x), which is in a different quadrant. This clarifies the importance of considering the sign and the quadrant the angle falls into.
-
Quadrant IV (270° < x < 360°): x lies in Quadrant IV, where sine is negative. (180° - x) lies in Quadrant III, also where sine is negative. The sine values are equal.
This quadrant-by-quadrant analysis reinforces the importance of understanding the sign of trigonometric functions in different quadrants and clarifies any apparent discrepancies.
Applications of the Identity: Solving Trigonometric Equations
The identity sin x = sin (180° - x) is invaluable in solving trigonometric equations. Consider an equation like:
sin x = 0.5
The principal solution is x = 30°. However, using the identity, we can find another solution:
x = 180° - 30° = 150°
This highlights that trigonometric equations often have multiple solutions within the range of 0° to 360°. The identity allows us to systematically find all these solutions.
Applications in Physics and Engineering
The sine function models many periodic phenomena in physics and engineering, such as:
-
Simple Harmonic Motion: The displacement of a mass on a spring or a pendulum can be modeled using sine functions. The identity helps in analyzing the motion at different points in the cycle.
-
Wave Propagation: Sine waves describe various wave phenomena like sound waves, light waves, and electromagnetic waves. The identity aids in understanding wave interference and superposition.
-
AC Circuits: Alternating current (AC) circuits involve sinusoidal voltages and currents. The identity simplifies analysis and calculations in these circuits.
Extending the Concept: Generalizations and Related Identities
The identity sin x = sin (180° - x) is a specific case of a more general identity:
sin (nπ ± x) = ± sin x, where n is an integer.
This general identity encompasses various symmetries and periodicities of the sine function. It demonstrates the cyclical nature of sine waves and their repetitive pattern over intervals of 2π (or 360°).
Frequently Asked Questions (FAQ)
Q1: Is the identity sin x = sin (180° - x) true for all values of x?
A1: Yes, it's true for all real values of x, but remember to consider the signs based on the quadrant.
Q2: Can this identity be used to solve equations involving other trigonometric functions?
A2: Indirectly, yes. You can use this identity to simplify equations that involve combinations of sine functions, leading to easier solutions.
Q3: What is the relationship between this identity and the concept of reference angles?
A3: The reference angle is the acute angle formed between the terminal side of an angle and the x-axis. This identity is directly related to finding equivalent sine values using reference angles. The sine of an angle and its reference angle are the same in magnitude, differing only in sign depending on the quadrant.
Q4: How does this identity relate to the cosine function?
A4: There's a related identity for cosine: cos x = -cos (180° - x). This highlights the difference in symmetry between sine and cosine functions. Sine is symmetric about the y-axis, while cosine is symmetric about the x-axis.
Q5: Are there similar identities for other trigonometric functions like tangent and cotangent?
A5: Yes, similar identities exist for other trigonometric functions. For example, tan x = -tan (180° - x). These identities are derived using the definitions of these functions in terms of sine and cosine.
Conclusion: A Foundation for Deeper Trigonometric Understanding
The identity sin x = sin (180° - x) is a fundamental concept in trigonometry with wide-ranging applications. Its elegant simplicity belies its power in solving trigonometric equations, analyzing periodic phenomena, and simplifying complex expressions. By understanding its derivation, graphical representation, and applications across various fields, you establish a solid foundation for further exploration into the fascinating world of trigonometry and its relevance in diverse scientific and engineering disciplines. This identity serves as a cornerstone for more advanced trigonometric concepts and techniques, emphasizing the beauty and practicality of mathematical relationships. Remember to practice applying this identity to various problems to fully grasp its implications and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
Height Of Mt Cook Nz
Sep 13, 2025
-
Vietnam Ho Chi Minh Trail
Sep 13, 2025
-
How To Write A Vignette
Sep 13, 2025
-
Map Of Huang He River
Sep 13, 2025
-
Europe In The 1500s Map
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Sin X Sin 180 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.