X 2 X 3 Expand
odrchambers
Sep 20, 2025 · 5 min read
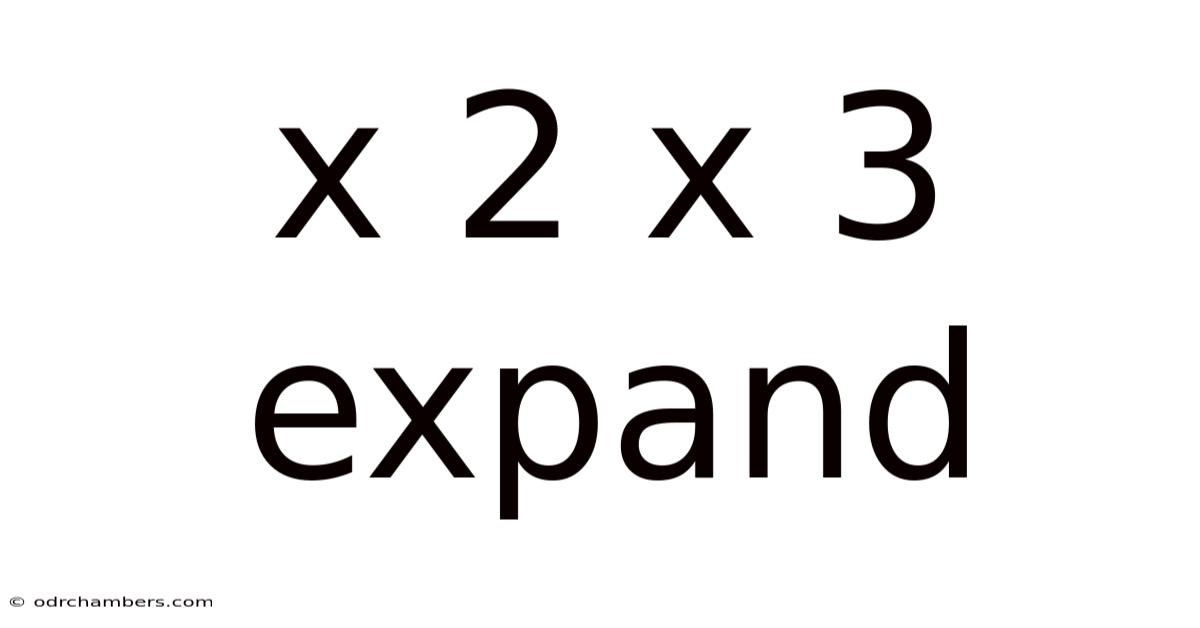
Table of Contents
Exploring the Expansive World of X² x 3: A Deep Dive into Algebraic Expansion and its Applications
This article delves into the seemingly simple algebraic expression, x² x 3, exploring its expansion, underlying principles, and diverse applications across various fields. We'll unpack the fundamental concepts, provide step-by-step explanations, and delve into more complex scenarios to build a solid understanding of this core algebraic concept. Understanding this seemingly basic operation is foundational to more advanced mathematical concepts and problem-solving.
Introduction: Unpacking the Basics
At its core, x² x 3 represents a multiplication problem involving an algebraic term (x²) and a constant (3). The expression can be expanded using basic algebraic rules, primarily focusing on the distributive property of multiplication over addition. Although this specific example is relatively simple, mastering its expansion forms the bedrock for understanding more complex polynomial multiplications and algebraic manipulations. This understanding is crucial for success in algebra, calculus, and numerous other scientific and engineering disciplines.
Step-by-Step Expansion of x² x 3
The expansion of x² x 3 is straightforward. We simply multiply the coefficient of the algebraic term (which is implicitly 1 in x²) by the constant:
-
Identify the terms: We have x² and 3.
-
Multiply the coefficients: The coefficient of x² is 1, and the constant is 3. Multiplying these gives us 1 x 3 = 3.
-
Combine the result with the variable: The variable remains unchanged, resulting in the expanded expression 3x².
Therefore, x² x 3 = 3x². This seemingly simple step lays the groundwork for more complicated algebraic manipulations.
Explanation Through the Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. While our example doesn't involve addition directly, we can consider the constant 3 as 3 x 1. This allows us to visualize the distributive property in action:
3 x x² = 3 x (x x x) This doesn't directly utilize the distributive property in its typical form, but it demonstrates that multiplication is commutative and associative, meaning the order doesn't matter.
Therefore, whether we see it as 3 multiplied by x², or x² multiplied by 3, the result remains consistently 3x².
Extending the Concept: Multiplying Polynomials
The principle of multiplying a monomial (a single term like x²) by a constant extends seamlessly to more complex polynomial multiplications. Let's consider a slightly more challenging example:
(2x² + 4x) x 3
Here, we apply the distributive property to each term within the parenthesis:
3 x (2x² + 4x) = (3 x 2x²) + (3 x 4x) = 6x² + 12x
This demonstrates how the same fundamental principle governs the expansion of more complex expressions. Each term within the parenthesis is multiplied by the constant outside the parenthesis.
Illustrative Examples and Practical Applications
The concept of expanding expressions like x² x 3 has wide-ranging applications across various disciplines:
-
Geometry: Calculating the area of a square with side length 'x' involves squaring the side length (x²). If we have three such squares, the total area is 3x².
-
Physics: In kinematics, calculating the distance traveled under constant acceleration often involves quadratic equations. Multiplying a quadratic term by a constant could represent scaling the acceleration or the duration of the motion.
-
Engineering: Many engineering problems involve solving equations with multiple variables and constants. The basic principles of algebraic expansion are frequently used to simplify and solve these equations. For example, calculating the volume of a cube multiplied by a factor is an essential problem solving scenario.
-
Finance: Compound interest calculations involve exponential growth, and understanding the expansion of algebraic expressions is crucial for modeling and predicting financial growth.
-
Computer Science: In algorithm analysis, evaluating the time or space complexity of an algorithm often involves working with polynomial expressions. The principles of expansion are necessary to simplify and analyze these expressions, often for assessing the scalability and efficiency of algorithms.
Advanced Concepts: Beyond Basic Expansion
While our focus has been on simple expansions, the underlying principles extend to far more complex scenarios:
-
Expanding Trinomials and Higher-Order Polynomials: The distributive property remains crucial when multiplying polynomials with three or more terms. Each term in the first polynomial must be multiplied by each term in the second. This process can become quite involved for high-order polynomials, and the use of techniques such as the FOIL method (First, Outer, Inner, Last) and visual aids can make the process manageable.
-
Expanding Expressions with Multiple Variables: Consider (2x²y + 3xy²) x 4. The same principles apply, resulting in 8x²y + 12xy². The variables are treated as separate algebraic entities, following the rules of exponents.
-
Factoring: The reverse process of expansion is factoring. This involves expressing a polynomial as a product of simpler terms. Understanding expansion is crucial for mastering factoring techniques.
-
Solving Equations: Expanding expressions is often a necessary step in simplifying and solving algebraic equations, which allows for finding the values of the variables that make the equation true.
Frequently Asked Questions (FAQ)
-
What if the constant is negative? The process is the same. For example, x² x (-3) = -3x². Simply incorporate the negative sign into the result.
-
Can I expand expressions with fractional constants? Absolutely. For example, x² x (1/2) = (1/2)x².
-
What about expressions with exponents other than 2? The same principle applies. For example, x³ x 5 = 5x³. The exponent remains unchanged during multiplication with a constant.
-
How do I handle more complex scenarios with multiple variables and exponents? The core principle of the distributive property remains. Carefully apply the distributive property to each term within the parenthesis. The use of the FOIL method or other similar methods can significantly simplify this process.
Conclusion: Mastering the Fundamentals
The seemingly straightforward expansion of x² x 3 is a foundational concept in algebra with broad applications. Mastering this fundamental skill builds a strong base for tackling more complex polynomial manipulations, equation solving, and problem-solving across numerous disciplines. Through understanding the distributive property and applying consistent steps, individuals can confidently navigate these algebraic concepts and successfully apply them to diverse real-world scenarios. The key lies not just in memorizing the process but in understanding the underlying principles and their practical implications, thereby building a strong foundation for future mathematical endeavors. Remember to practice regularly, using varied examples to solidify your understanding and build confidence in your algebraic skills.
Latest Posts
Latest Posts
-
Sheltie Breeders Puppies For Sale
Sep 20, 2025
-
List Of The Perfect Squares
Sep 20, 2025
-
10 Duties Of Barangay Captain
Sep 20, 2025
-
Ester Bond Vs Ether Bond
Sep 20, 2025
-
Commercial Kitchen For Lease Sydney
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 Expand . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.