Y 1 2x 1 Graph
odrchambers
Sep 23, 2025 · 7 min read
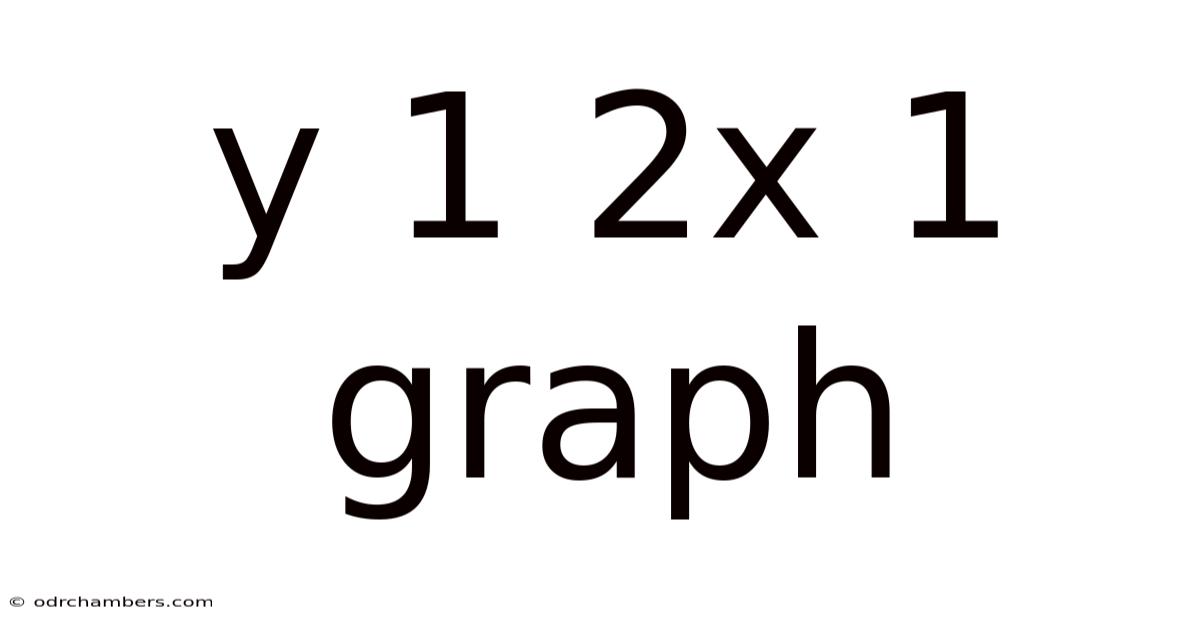
Table of Contents
Decoding the Graph of y = 1/2x + 1: A Comprehensive Guide
Understanding linear equations and their graphical representations is fundamental to grasping many concepts in algebra and beyond. This article delves into the specifics of the linear equation y = 1/2x + 1, exploring its characteristics, how to graph it, and its real-world applications. We'll move beyond simply plotting points and unpack the meaning behind the slope, y-intercept, and the overall shape of the line. This guide aims to provide a comprehensive understanding, suitable for both beginners and those seeking a refresher.
Introduction: Understanding the Equation y = 1/2x + 1
The equation y = 1/2x + 1 is a linear equation in the slope-intercept form, y = mx + b. This form is incredibly useful because it immediately reveals key characteristics of the line:
-
m (slope): Represents the rate of change of y with respect to x. In our equation, m = 1/2. This means for every 1 unit increase in x, y increases by 1/2 a unit. A positive slope indicates a line that rises from left to right.
-
b (y-intercept): Represents the point where the line intersects the y-axis (where x = 0). In our equation, b = 1. This means the line crosses the y-axis at the point (0, 1).
Understanding these two components is crucial for easily graphing the line and interpreting its meaning.
Graphing y = 1/2x + 1: A Step-by-Step Approach
There are several ways to graph this linear equation. We'll explore two common methods:
Method 1: Using the Slope and Y-intercept
-
Plot the y-intercept: Begin by plotting the point (0, 1) on the coordinate plane. This is where the line crosses the y-axis.
-
Use the slope to find another point: The slope is 1/2, which can be interpreted as "rise over run." This means for every 2 units you move to the right (run), you move up 1 unit (rise). Starting from the y-intercept (0, 1), move 2 units to the right and 1 unit up. This brings you to the point (2, 2).
-
Draw the line: Draw a straight line that passes through both points (0, 1) and (2, 2). Extend the line in both directions to represent the infinite nature of the linear equation.
Method 2: Using a Table of Values
This method involves creating a table of x and y values that satisfy the equation. Choose a few values for x, substitute them into the equation, and solve for the corresponding y values.
| x | y = 1/2x + 1 | (x, y) |
|---|---|---|
| -2 | 0 | (-2, 0) |
| 0 | 1 | (0, 1) |
| 2 | 2 | (2, 2) |
| 4 | 3 | (4, 3) |
| -4 | -1 | (-4, -1) |
Plot these points on the coordinate plane and draw a straight line connecting them. You'll find that it's the same line as the one obtained using the slope-intercept method.
Interpreting the Graph: Slope, Intercept, and the Line's Meaning
The graph of y = 1/2x + 1 is a straight line that slopes upward from left to right. Let's break down what this visually represents:
-
Positive Slope: The upward slope signifies a positive correlation between x and y. As x increases, y also increases. This is a direct relationship.
-
Y-intercept (0, 1): The y-intercept indicates the value of y when x is zero. In a real-world context, this could represent an initial value or a starting point.
-
Rate of Change: The slope of 1/2 represents the rate at which y changes with respect to x. It's a constant rate of change, meaning the line maintains a consistent slope throughout.
Real-World Applications: Where Does This Equation Show Up?
Linear equations like y = 1/2x + 1 appear in many real-world scenarios. Here are a few examples:
-
Cost Calculation: Imagine a taxi fare where the initial fare is $1 (y-intercept) and the cost per kilometer is $0.50 (slope). The equation y = 0.5x + 1 can then model the total cost (y) based on the distance traveled (x).
-
Growth Models: Simple linear growth, such as the growth of a plant at a constant rate, can be represented by a linear equation. The y-intercept would represent the initial height, and the slope would represent the growth rate per unit of time.
-
Conversion Rates: Converting units, such as Celsius to Fahrenheit (though a slightly more complex linear equation is needed for this), can be modeled linearly, with the slope and y-intercept representing the conversion factors.
Extending the Understanding: Parallel and Perpendicular Lines
The equation y = 1/2x + 1 belongs to a family of lines. Understanding its relationship with other lines enhances the overall comprehension.
-
Parallel Lines: Any line with a slope of 1/2 will be parallel to y = 1/2x + 1. Parallel lines never intersect. They have the same slope but different y-intercepts. For example, y = 1/2x + 5 is parallel to y = 1/2x + 1.
-
Perpendicular Lines: A line perpendicular to y = 1/2x + 1 will have a slope that is the negative reciprocal of 1/2, which is -2. Perpendicular lines intersect at a 90-degree angle. For example, y = -2x + 3 is perpendicular to y = 1/2x + 1.
Solving Equations Involving y = 1/2x + 1
Solving equations often involves finding the intersection points of lines. Here are a few examples of how to solve equations involving y = 1/2x + 1:
Example 1: Finding the intersection with another line.
Let's find the intersection point of y = 1/2x + 1 and y = x - 1. Since both equations are solved for y, we can set them equal to each other:
1/2x + 1 = x - 1
Solving for x:
1/2x = x -2
-1/2x = -2
x = 4
Substitute x = 4 back into either equation to find y:
y = 1/2(4) + 1 = 3
The intersection point is (4, 3).
Example 2: Finding the x-intercept.
The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, set y = 0 in the equation:
0 = 1/2x + 1
-1 = 1/2x
x = -2
The x-intercept is (-2, 0).
Frequently Asked Questions (FAQ)
Q: What is the domain and range of the function y = 1/2x + 1?
A: The domain (all possible x values) is all real numbers (-∞, ∞). The range (all possible y values) is also all real numbers (-∞, ∞).
Q: Is y = 1/2x + 1 a function?
A: Yes, it is a function. For every input value of x, there is only one corresponding output value of y. This satisfies the definition of a function.
Q: How can I use this equation in a spreadsheet program like Excel?
A: You can easily plot this line in Excel by creating a table of x and y values (as in Method 2 above) and then using the chart feature to create a scatter plot with a line connecting the points.
Q: Can this equation be used to model non-linear relationships?
A: No, this specific equation models a linear relationship. For non-linear relationships, you would need different types of equations (quadratic, exponential, etc.).
Conclusion: Mastering Linear Equations and Their Graphs
The equation y = 1/2x + 1, seemingly simple at first glance, provides a rich foundation for understanding linear functions and their graphical representations. By grasping the concepts of slope and y-intercept, you can not only accurately plot the line but also interpret its meaning in various real-world applications. Remember to practice different graphing techniques and work through examples to solidify your understanding. The ability to interpret and manipulate linear equations is a vital skill in mathematics and beyond, laying the groundwork for more advanced mathematical concepts. With continued practice and exploration, you will build a strong foundation in this critical area of mathematics.
Latest Posts
Latest Posts
-
Integration Of Inverse Trigonometric Functions
Sep 23, 2025
-
Dinosaurs That Begin With A
Sep 23, 2025
-
Web Of Dreams Casteel Series
Sep 23, 2025
-
Garlic And Rosemary Roast Potatoes
Sep 23, 2025
-
Forest Hill Shopping Centre Victoria
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Y 1 2x 1 Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.